 Тесты
Тесты Эту задачу опубликовали в нескольких популярных соцсетях и стали активно её обсуждать и решать. Причём ответы были разные. А сможете ли вы её решить?
Логическая задача
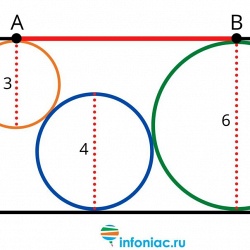
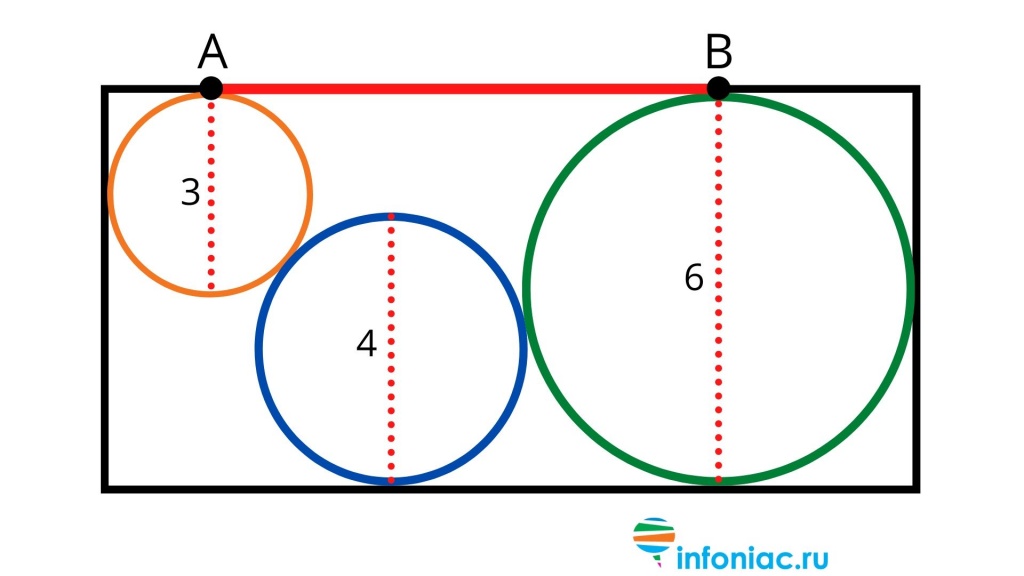
Перед вами рисунок прямоугольника (см. ниже), внутри которого три круга.
-
Диаметр одного круга три, другого четыре, и третьего шесть.
-
Первый круг касается двух сторон прямоугольника и второго круга.
-
Второй круг касается одной стороны прямоугольника, а также первого и второго кругов.
-
Третий круг касается всех трёх сторон прямоугольника и второго круга.
Вам предлагается найти отрезок, который соединяет точку касания первого круга и третьего (см. картинку). Чему равен отрезок AB?
Решение задачки вы найдёте ниже.
Смогли решить?
На самом деле все не так сложно.
Читайте также: 7 странных головоломок, которые можно услышать на собеседовании
Бонус
Перед тем, как мы перейдём к решению, мы приготовили для вас бонусную простую задачку на логику:
В одном зоопарке есть пингвины и львы. Если посчитать всех пингвинов и львов, то получим 72 животных, и у всех в сумме 200 ног. Сколько пингвинов в зоопарке?
Пишите свои ответы в комментариях. Там же вы узнаете и ответ на эту задачку.
Ответ и решение головоломки с кругами
Ответ: 3√6 см≈ 7,35 см
Решение:
Шаг 1
Нам нужно найти расстояние между диаметрами оранжевого круга и зелёного. Это расстояние в итоге станет частью отрезка, длину которого нам надо найти.
Мы знаем, что радиус первого круга 1,5, второго 2, а третьего 3.
-
Но для начала найдём расстояние от диаметра зелёного до диаметра синего круга. Для этого построим прямоугольный треугольник (см. картинку).
-
Один катет будет равен 3 (радиус зелёного круга) – 2 (радиус синего круга) = 1.
-
Так как эти два круга касаются друг друга, то гипотенуза нашего треугольника будет равна сумме радиусов этих кругов, то есть 2 + 3 = 5.
-
По теореме Пифагора находим большой катет, который и является расстоянием между диаметрами двух кругов, (и по совместительству частью отрезка, который нам нужен): √52 - √12 = √24 = 2√6
Шаг 2
Теперь найдём расстояние между диаметрами оранжевого и синего кругов. Это расстояние в итоге станет второй частью отрезка, длину которого нам надо найти.
Для этого снова построим прямоугольный треугольник.
-
Заметьте, что над синим кругом есть отрезок, равный 1,5 (т.к. он равен радиусу оранжевого круга), а радиус синего круга 2. Чтобы узнать длину одного катета, нужно из всей ширины прямоугольника (она равна диаметру зелёного круга) отнять верхний кусочек на 1,5 и диаметр синего круга. Получается (3+3) – 2 – 1,5 = 2,5.
-
Так как круги соприкасаются, то гипотенуза треугольника равна сумме радиусов, то есть 1,5 + 2 = 3,5. По теореме Пифагора находим длину второго катета: √3,52 - √2,52 = √6.
Шаг 3
Осталось соединить два отрезка: √6 + 2√6 = 3√6, что примерно равно 7,35 .


















{x+y=72; 2x+4y=200
2(72-y)+4y=200
144-2y+4y=200
2y=200-144
y=28
x=72-28=44
44*2+28*4=88+112=200
А в этом решении уже не простая задача на логику.