Тесты
Тесты Два очень умных муравья – Макс и Роза – очень любят соревноваться, однако передвигаются оба всегда с одинаковой скоростью, поэтому у них всегда ничья.
Они решили придумать такой забег с препятствиями, чтобы один из них обязательно выиграл.
Для этого у них есть две коробки – два кубоида (прямоугольные параллелепипеды), по одной коробке для каждого.
По этим коробкам они должны передвигаться как можно быстрее, чтобы добраться до противоположного угла, начиная с нижнего угла своей коробки.
Вот размеры каждой коробки:

Если каждый из них выберет самый короткий путь до противоположного угла, кто доберётся до финиша первым?
(Не забывайте, что они муравьи, поэтому могут легко забираться куда угодно, ходить смело по краям или бокам коробки)
Правильный ответ и решение вы найдёте чуть ниже.
Читайте также: Головоломка с кругами, которую многие в соцсетях не могли решить
.
.
.
Правильный ответ на задачу
Роза будет первой, если найдёт самый короткий путь
Решение:
Нам нужно найти длину самых коротких путей. Самый простой способ это сделать – выпрямить коробки. Как только вы это сделаете, найти кратчайший путь будет очень просто. Самый короткий путь – это прямая линия.
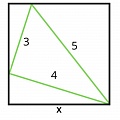
В случае с Максом, если развернуть куб и нарисовать прямую линию от старта до финиша, то можно посчитать расстояние с помощью теоремы Пифагора.
Один катет равен 3+3=6 см, а второй 3 см, значит гипотенуза равна √45 см.

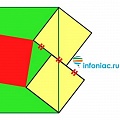
В случае с Розой есть три возможности раскрыть и выпрямить коробку. Все три представлены в картинке.

По теореме Пифагора узнаём длину красной линии.
-
В первом случае это: √ (2+4) + √3 = √45 см.
-
Во втором случае это: √(2+3) + √4 = √41 см.
-
С третьем случае это: √(4+3) + √2 = √53.
Самый короткий путь Розы равен √41 см или около 6,4 см, а самый короткий путь Макса √45 см или 6,7 см. Значит Роза будет первой. Для этого ей нужно пройти вот этот путь: