 Тесты
Тесты Такие геометрические головоломки уже стали популярными в Японии.
Их придумал Наоки Инаба (Naoki Inaba), известный создатель логических головоломок, чьи работы публикуются в различных журналах.
Свою первую головоломку он придумал после просьбы директора школы создать логическую задачку.
Инаба называет работы Menseki meiro (можно перевести как "паутина площадей"). В них вам нужно найти площадь прямоугольника, его длину или ширину.
Правила:
-
Можно использовать только формулу вычисления площади прямоугольника, то есть S = a * b (a - длина, b - ширина). Нельзя использовать десятичные дроби. Нельзя использовать уравнения с неизвестными. Используйте только целые числа.
-
Можно дополнять рисунки.
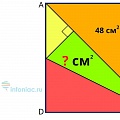
Задачка 1 (для разогрева)
Ответ в конце теста.

Читайте также: Шпионский тест: Только человек с нестандартным мышлением сможет найти секретное слово
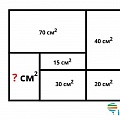
Задача 2

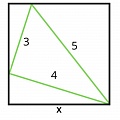
Задача 3

Ответы:
Задача 1.
Ответ: 5 см.
Дорисовываем синий прямоугольник. Стороны у него 4 и 5, а значит площадь 20. Соединяем с площадью маленького прямоугольника и получаем 36 [20 + 16]. Такая же площадь большого прямоугольника.
Поскольку они имеют одинаковую высоту, они должны иметь одинаковую ширину, а значит ширина большого прямоугольника равна 5 см.
Задача 2
Ответ: 20 кв. см.
Длина отрезка X равна: (38 + 39) / 7 = 77/7 = 11 см
Длина отрезка Y равна: 11 - 4 = 7 см
Длинна отрезка Z равна: 7 + 3 = 10 см
Следовательно, недостающее значение (10 x 6) - 40 см2 = 20 см2
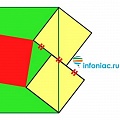
Второй вариант решения:
Дорисовываем синие вспомогательные прямоугольники. Нам нужно узнать площадь всего большого прямоугольника, в который входят все фигуры. Для этого нам нужно узнать его длину и ширину.
1. Узнаём длину:
1.1. Общая площадь верхних двух прямоугольников равна: 38 + 39 =77. Если ширина 7, значит длина этого общего прямоугольника 77:7=11.
1.2. Длинна маленького верхнего отрезка 3, а значит длина всего большого прямоугольника 11 + 3 = 14
2. Узнаём ширину:
Часть ширины равна 7, а другая часть равна 6, значит ширина всего большого прямоугольника равна 13.
3. Площадь большого прямоугольника: 14 х 13 = 182.
4. Площадь нижнего синего прямоугольника: 6 х 4 = 24
5. Площадь верхнего синего прямоугольника: 3 х 7 =21.
6. Отнимаем от всей площади, те площади, которые знаем, и получаем площадь серого прямоугольника: 182 – 77 – 40 – 21 – 24 = 20.
Задача 3
Ответ: 10 см.
1. Сначала мы можем сделать вывод, что длина синего прямоугольника равна 5 см, поскольку 4 x 5 = 20.
2. Площадь синего прямоугольника равна: 5 х 5 = 25 см.
3. Таким образом, зелёный прямоугольник имеет площадь 25 + 14 = 39 см.
4. Площадь большого прямоугольника 78, то есть в два раза больше чем общая площадь маленьких (78 : 39 =2).
4. Поскольку зелёный прямоугольник и чёрный имеют одинаковую высоту, неизвестный отрезок должен быть в два раза больше ширины зелёного прямоугольника, то есть 2 x 5 = 10 см.

















1. 20:4=5
2. 14:5=2,8
3. 5+2,8=7,8
4. 78:7,8=10